いつもお世話になっております、沖縄で中古住宅扱う株式会社イエカリヤ代表の當間です。
昨日に引き続き宅建試験に出る計算問題の基本とコツを書いていきます。
今日の所はそこまで多く出るところではないので、時間に余裕がある方だけでいいと思います。
●こんな時に比率の問題がでてくる
相続の問題でおそらく一番面倒なのが、父母のどちらか一方を同じくする兄弟姉妹の相続です。
昨日お話した分数の掛け算は、よく出るのでなんとなく覚えるのですが、今回のお話はたまにしか見ないですし計算方法も慣れていないので苦手意識をお持ちの方も多いかと思います。
前提として。
・子と直系尊属(両親鵜や祖父母)がいない。
・父母のどちらか一方を同じくする兄弟姉妹(いわゆる腹違い)がいる。
・両親を同じくする兄弟姉妹に比べて、どちらか一方を同じくする兄弟姉妹の法定相続分は半分になる。
初めてこのお話をする時、よく誰が亡くなったかを勘違いする方が多いので、少しゆっくり説明します。

今回のお話この場合に、Cさんが亡くなった時のお話です。(D、Eさんでも同じです。)
よく勘違いしがちなのがBさんが亡くなった時ですが、この場合の子供たちの法定相続分に差はありません。
BさんからするとC、D、E、Gは実子に違いないので通常通りの分配でいいんです。
先ほども書いたように今回のケースは、子(第一順位)もおらず、親や祖父母もいない(直系尊属、第二順位)、兄弟姉妹(第三順位)がいるじょうたいですね。
両親を同じくする兄弟姉妹のみであれば、等分したらいいのですが、今回は片方の親だけが同じGさんがいます。
宅建の勉強をしていれば前提知識として、両親を同じくする兄弟姉妹に比べて、どちらか一方を同じくする兄弟姉妹の法定相続分は半分になる。ということを知っている方は多いと思いますが、具体的な計算はイマイチという方もいらっしゃると思います。
少しだけ、問題から離れて比率の計算の基本と宅建で解くときのちょっとしたコツを書いていきます。
●比率の求め方
例えば、3,000円を甲さん2、乙さん1の割合で分けるとしましょう。
これくらいであればパッと甲さん2,000円、乙さん1,000円で分けるということがわかると思います。
簡単な分け方であれば頭の中でやってしまいますが、金額が12,000円なら?比率が7対5なら?丙さんが出てきたら?計算できますか?
何をやっているか分解してみましょう。
甲さん2、乙さん1で分ける場合。
式で書くと。
甲:乙=2:1
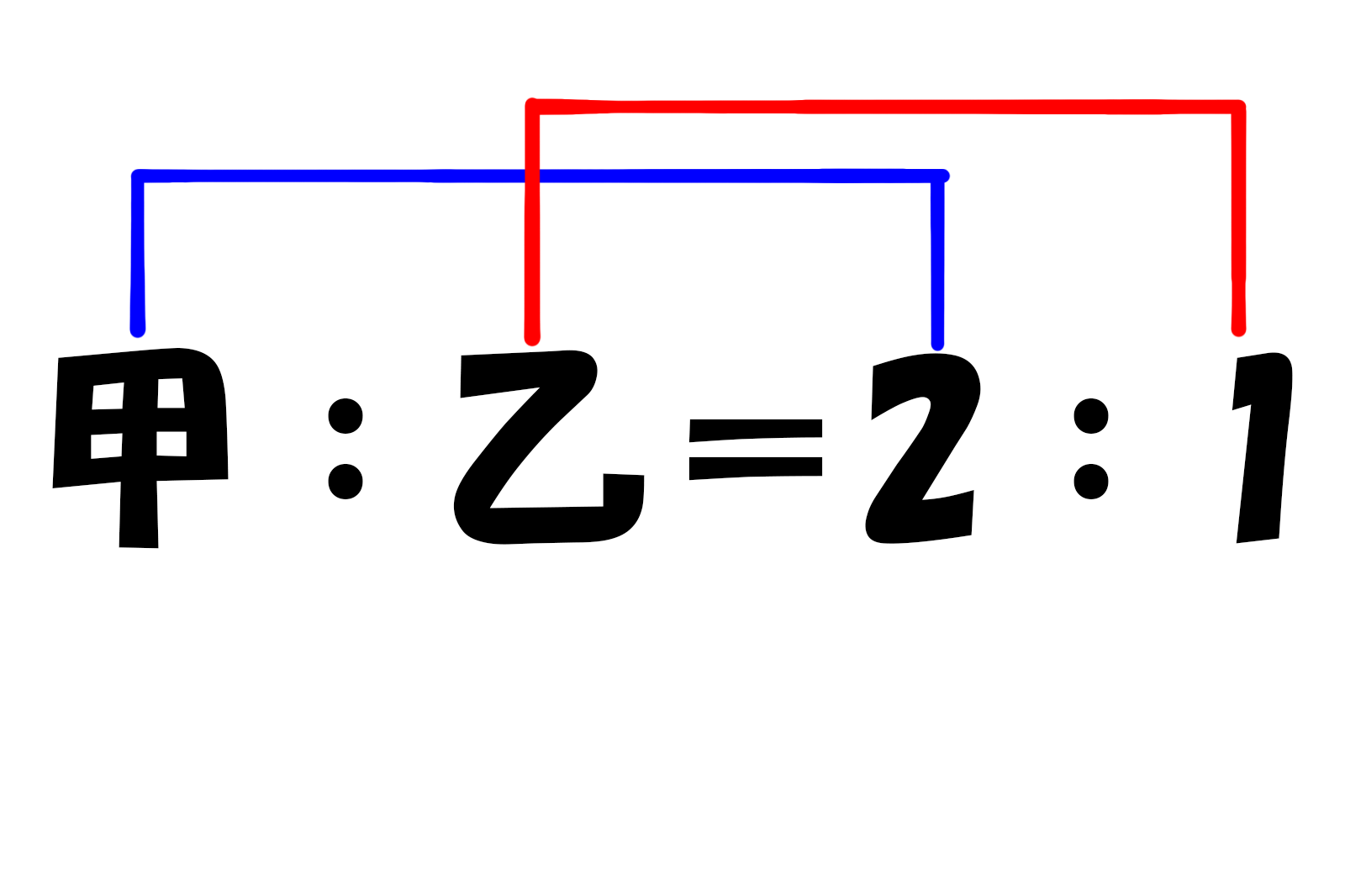
こうなります。
ここで書いてある2:1は全体の中からどれだけもらえるのかという数字になります。
で、全体って何?というと出てきた比率の数を足した数になります。
今回のケースだと2+1=3ですね。
なので、甲さんは3分の2を貰えて、乙さんは3分の2を貰えることになります。
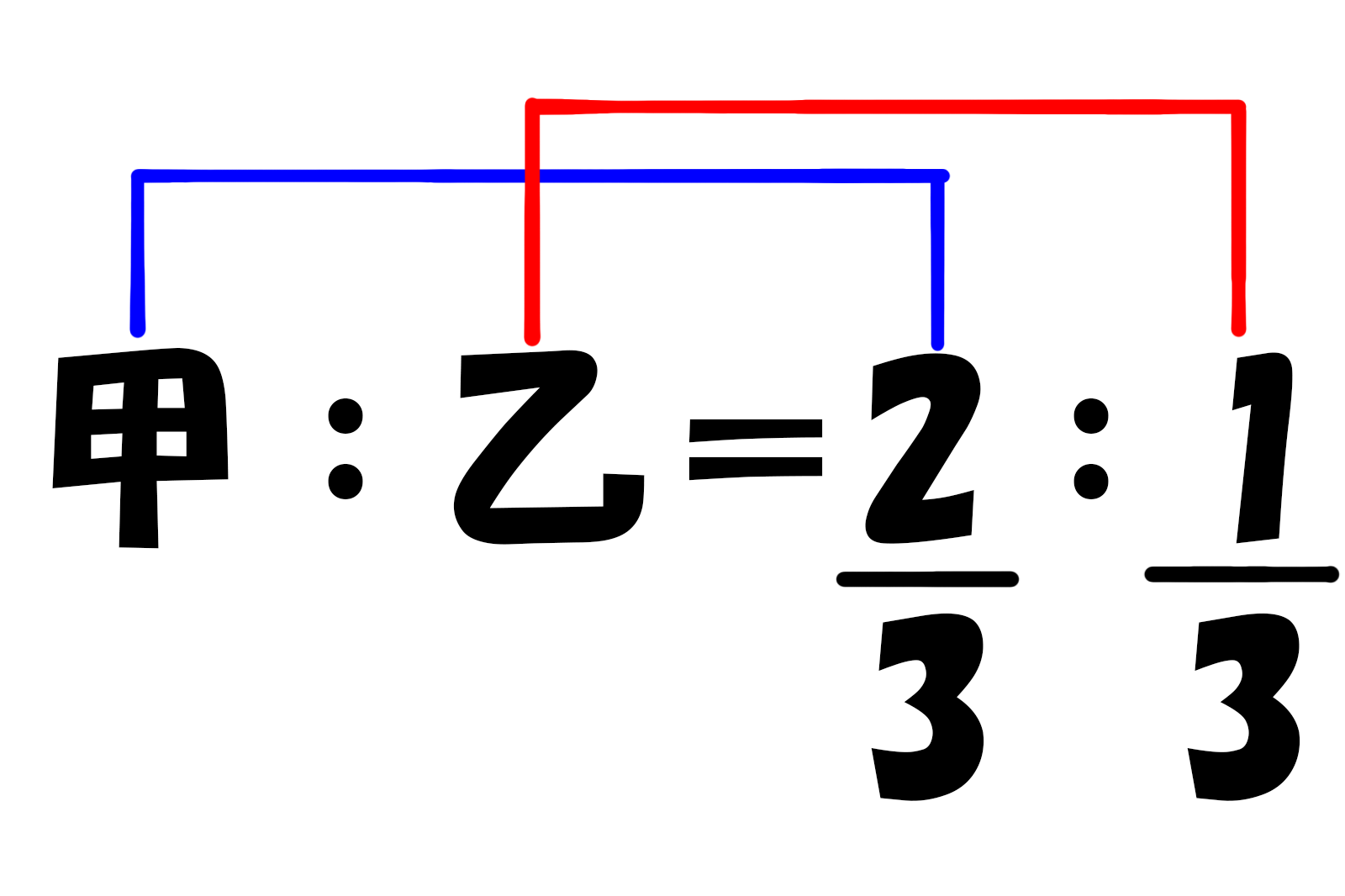
なので3,000円の内から甲さんがもらえるのは。
3,000×3分の2=2,000円。
乙さんがもらえるのは
3,000×3分の1=1,000円。
1,000円ということになります。
もし12,000円だとすると
甲は12,000×3分の2=8,000円
乙は12,000×3分の2=4,000円になります。
もし、12,000円を7:5で分けたければ
7+5=12なので
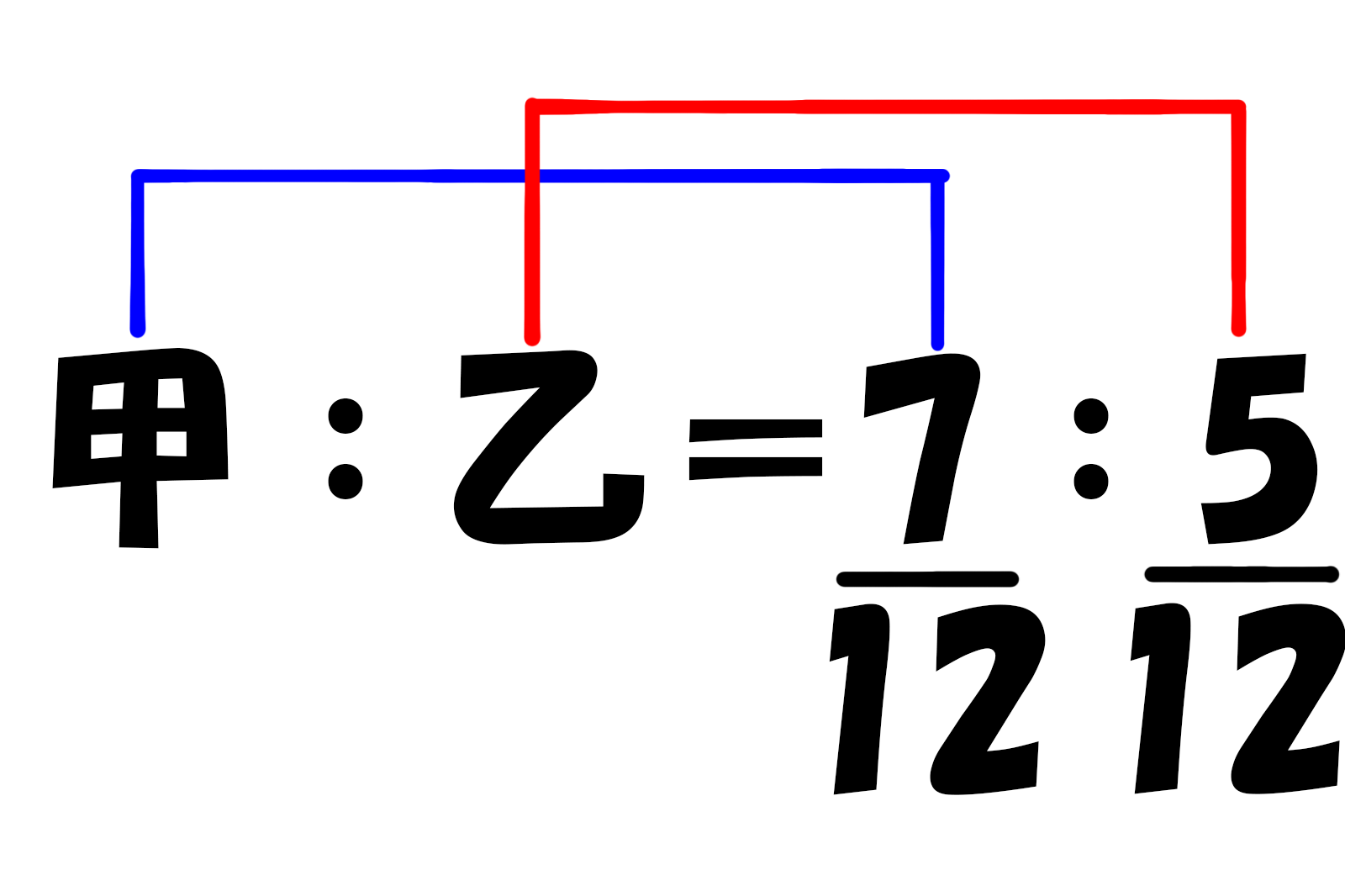
甲は12,000円×12分の7=7,000円
乙は12,000円×12分の5=5,000円
という風にパッと見複雑な分け方でもスムーズに解くことができます。
これは複数人数でも同じように表せます。
丙さんもいたとして。
甲さん2、乙さん1、丙さん1で分けるとすると、式は。
甲:乙:丙=2:1:1
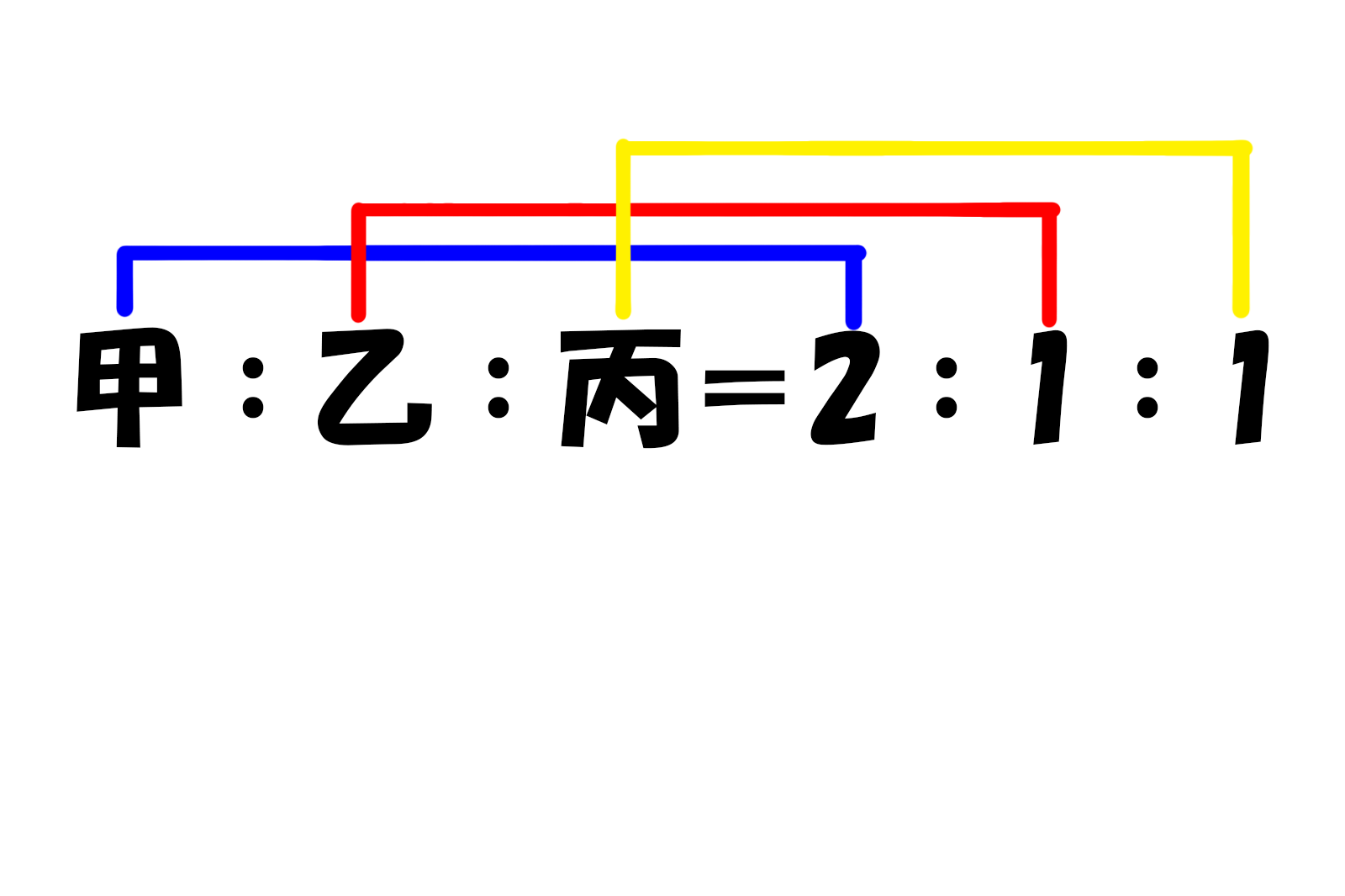
になります。
なので全体は
2+1+1=4ですね。
ということは甲さん4分の2、乙さんと丙さんは4分の1ずつになります。
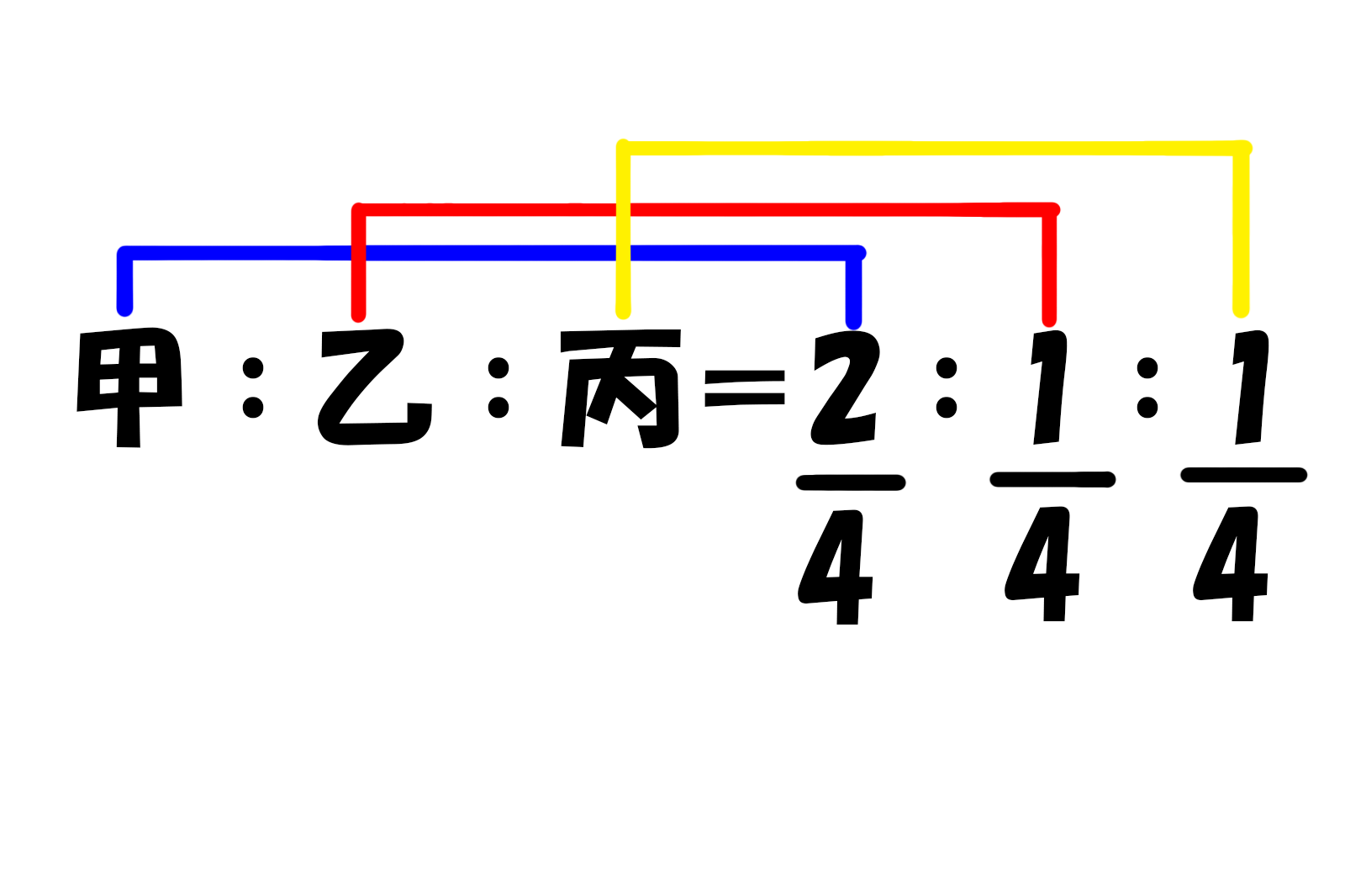
●宅建用のコツ
ここまでが比率の計算の基本でした、宅建の問題を解くにあたって、小学生の時に教えてもらった方法とは少し変えた方が楽になるんです。
そのコツが「式を右と左に分けない」です。

先ほどの基本ではこういう風に書きましたし、学校でも式は右と左で分けて書くように教えられたと思います。
今回はわかりやすく色を分けて対応するように結びましたが、試験中にそんなことするのは面倒です。
登場人物が2人ならいいんですけど、3人4人と増えていくとどの比率が誰に対応しているのか少しわかりにくくなりますよね?
そんな時、あえて式の右側を左側の下に持っていきます。

すると、どの数字が誰に対応しているかが一目瞭然ですね。
さらに、線を引っ張って全体の数字を入れれば、分数まできれいに出来上がります。

教科書通りに計算するよりもこちらの方がわかりやすいですよね。
思っていたよりも長くなってしまったので、先ほどの問題は後日ブログで実際に解いていきます。
●まとめ
・相続の問題で比率を求めることがある
・比率と人物を上下に並べるとわかりやすい